हेप्टागोनल प्रिज़्म सुविधाएँ और वॉल्यूम की गणना कैसे करें

एक हेप्टागोनल प्रिज़्म एक ज्यामितीय आकृति है, जैसा कि नाम से पता चलता है, इसमें दो ज्यामितीय परिभाषाएँ शामिल हैं: प्रिज़्म और हेप्टागन.

एक "प्रिज़्म" एक ज्यामितीय आकृति है जो दो आधारों द्वारा सीमित होती है जो समान और समानांतर बहुभुज होते हैं और उनके पार्श्व चेहरे समांतर चतुर्भुज होते हैं.

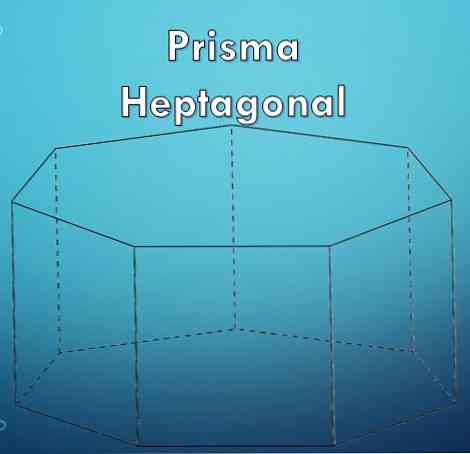
एक "हेप्टागन" एक बहुभुज है जो सात (7) पक्षों से बनता है। चूंकि एक हेप्टागन एक बहुभुज है, इसलिए यह हो सकता है कि यह नियमित या अनियमित हो.

एक बहुभुज को नियमित कहा जाता है यदि उसके सभी पक्षों की लंबाई समान होती है और उनके आंतरिक कोण समान होते हैं, तो उन्हें समभुज बहुभुज भी कहा जाता है; अन्यथा यह कहा जाता है कि बहुभुज अनियमित है.

एक हेप्टागोनल प्रिज्म के लक्षण

कुछ विशिष्ट विशेषताएं निम्नलिखित हैं जिनमें एक हेपटागोनल प्रिज़्म है जैसे: इसका निर्माण, इसके ठिकानों के गुण, इसके सभी चेहरों का क्षेत्रफल और इसकी मात्रा.

1- निर्माण

हेप्टागोनल प्रिज्म के निर्माण के लिए दो हेप्टैगन की आवश्यकता होती है, जो कि इसके आधार और सात समांतर चतुर्भुज होंगे, जो हेप्टागन के प्रत्येक तरफ एक होते हैं.

एक हेप्टागन ड्राइंग द्वारा शुरू करें, फिर समान लंबाई के सात ऊर्ध्वाधर रेखाएं खींचें, जो इसके प्रत्येक कोने से आती हैं.

अंत में एक और हेप्टागन खींचा जाता है ताकि उसके शीर्ष पिछले चरण में खींची गई रेखाओं के अंत के साथ मेल खाते हों.

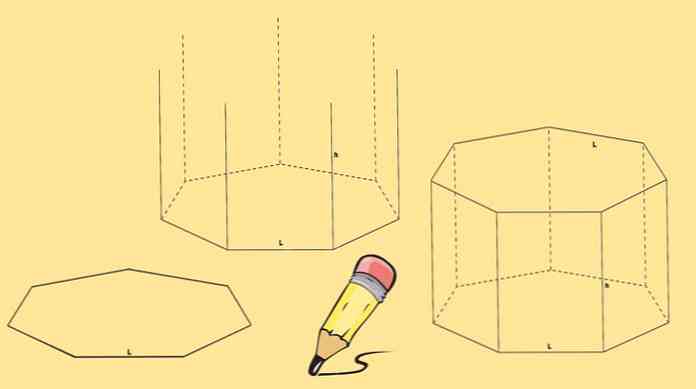
ऊपर खींचे गए हेप्टागोनल प्रिज्म को स्ट्रेट हेप्टागोनल प्रिज्म कहा जाता है। लेकिन आप भी निम्न आकृति में एक की तरह एक तिरछा हेपटागोनल प्रिज्म रख सकते हैं.

2- इसके आधारों के गुण

चूँकि उनके आधार हेप्टैगन हैं, वे इस बात का अनुपालन करते हैं कि विकर्ण संख्या D = nx (n-3) / 2 है, जहाँ "n" बहुभुज के पक्षों की संख्या है; इस मामले में हमारे पास डी = 7 × 4/2 = 14 है.

हम यह भी देख सकते हैं कि किसी भी हेप्टागन (नियमित या अनियमित) के आंतरिक कोण का योग बराबर 900º है। यह निम्न छवि द्वारा सत्यापित किया जा सकता है.

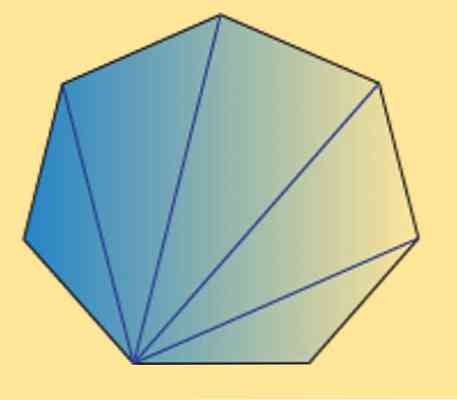
जैसा कि आप देख सकते हैं, 5 आंतरिक त्रिकोण हैं, और एक त्रिकोण के आंतरिक कोणों का योग 180 there के बराबर है, यह प्राप्त किया जा सकता है कि वांछित परिणाम.

3- हेप्टागोनल प्रिज्म के निर्माण के लिए आवश्यक क्षेत्र

चूंकि इसके आधार दो हेप्टैगन हैं और इसके किनारे सात समांतर चतुर्भुज हैं, एक हेपटागोनल प्रिज्म के निर्माण के लिए आवश्यक क्षेत्र 2xH + 7xP के बराबर है, जहां "H" प्रत्येक हेपटागन का क्षेत्र है और "P" प्रत्येक समांतर चतुर्भुज का क्षेत्र है।.

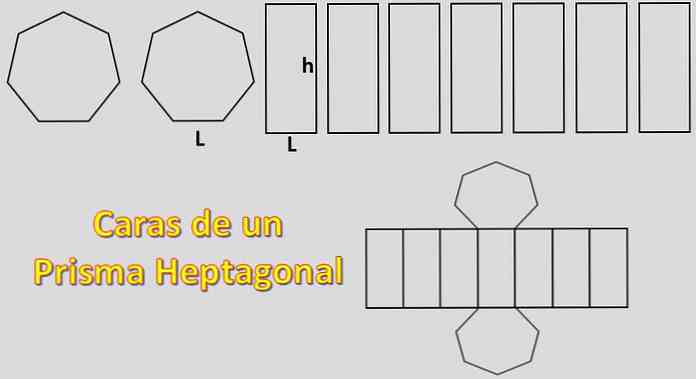
इस मामले में, एक नियमित हेप्टागन के क्षेत्र की गणना की जाएगी। इसके लिए अपोतमा की परिभाषा जानना जरूरी है.

एपोटेम एक लंब रेखा है जो एक नियमित बहुभुज के केंद्र से इसके किसी भी पक्ष के मध्य बिंदु तक जाती है.

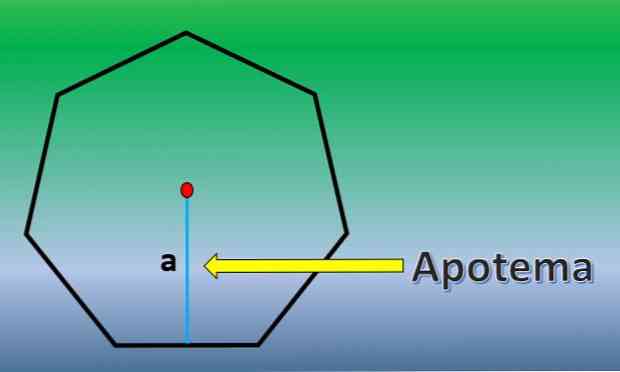
एक बार एपोटेम ज्ञात होने के बाद, हेप्टागन का क्षेत्र H = 7xLxa / 2 है, जहां "L" प्रत्येक पक्ष की लंबाई और "a" एपोटेम की लंबाई है।.

समांतर चतुर्भुज का क्षेत्रफल गणना के लिए आसान है, P = Lxh के रूप में परिभाषित किया गया है, जहां "L" हेपटागन के किनारे की समान लंबाई है और "h" प्रिज्म की ऊंचाई है.

अंत में, हेपटागोनल प्रिज्म (नियमित आधारों के साथ) बनाने के लिए आवश्यक सामग्री की मात्रा 7xLxa + 7xLxh है, अर्थात 7xL (a + h).

4- मात्रा

एक बार जब आधार का क्षेत्र और प्रिज्म की ऊंचाई ज्ञात की जाती है, तो वॉल्यूम को (बेस एरिया) x (ऊंचाई) के रूप में परिभाषित किया जाता है.

एक हेपटागोनल प्रिज्म (नियमित आधार के साथ) के मामले में यह है कि इसकी मात्रा V = 7xLxaxh / 2 है; V = Pxaxh / 2 के रूप में भी लिखा जा सकता है, जहां "P" नियमित हेप्टागोन की परिधि है.

संदर्भ

1. बिलस्टीन, आर।, लिब्सेकिंड, एस।, और लोट, जे। डब्ल्यू। (2013). गणित: बेसिक शिक्षा शिक्षकों के लिए एक समस्या को हल करने का तरीका. लोपेज़ मेटोस एडिटर्स.
2. फ्रीगोसो, आर.एस., और कैरेरा, एस। ए। (2005). गणित ३. संपादकीय प्रोग्रेसो.
3. गैलार्डो, जी।, और पिलर, पी। एम। (2005). गणित ६. संपादकीय प्रोग्रेसो.
4. गुतिरेज़, सी। टी। और सिस्नेरोस, एम। पी। (2005). तीसरा गणित पाठ्यक्रम. संपादकीय प्रोग्रेसो.
5. किन्से, एल।, और मूर, टी। ई। (2006). समरूपता, आकार और स्थान: ज्यामिति के माध्यम से गणित का एक परिचय (सचित्र, पुनर्मुद्रण संस्करण।) स्प्रिंगर विज्ञान और व्यापार मीडिया.
6. मिशेल, सी। (1999). चमकदार मैथ लाइन डिजाइन (इलस्ट्रेटेड एड।)। स्कोलास्टिक इंक.
7. आर।, एम। पी। (2005). मैं 6º आकर्षित करता हूं. संपादकीय प्रोग्रेसो.