कोलिनियर सिस्टम और उदाहरण

कोलिनियर वैक्टर वे मौजूदा वैक्टर के तीन प्रकारों में से एक हैं। यह उन वैक्टर के बारे में है जो एक ही दिशा या कार्रवाई की रेखा में हैं। इसका मतलब निम्नलिखित है: दो या दो से अधिक वैक्टर को एक दूसरे के समानांतर होने वाली सीधी रेखाओं में व्यवस्थित किया जाता है.

एक वेक्टर को एक शरीर पर लागू मात्रा के रूप में परिभाषित किया गया है और एक दिशा, एक भावना और एक पैमाने के रूप में विशेषता है। वैक्टर विमान या अंतरिक्ष में पाए जा सकते हैं और विभिन्न प्रकार के हो सकते हैं: कोलिनियर वैक्टर, समवर्ती वैक्टर और समानांतर वैक्टर.

सूची

• 1 कोलिनियल वैक्टर
• २ लक्षण
  • २.१ उदाहरण १
  • २.२ उदाहरण २
  • २.३ उदाहरण १
• 3 कोलिनियर वेक्टर सिस्टम
  • 3.1 विपरीत इंद्रियों के साथ कोलिनियर वैक्टर
  • 3.2 कोलिनियर वैक्टर समान भाव से
  • 3.3 समान परिमाण और विपरीत इंद्रियों के साथ कोलिनियर वैक्टर
• 4 कोलिनियर और समवर्ती वैक्टर के बीच अंतर
• 5 संदर्भ

कोलिनियर वैक्टर

वैक्टर के एक दूसरे की कार्रवाई की लाइन बिल्कुल वैसी ही होती है, जैसा कि सभी वैक्टरों में से प्रत्येक के आकार और अर्थ की परवाह किए बिना, अन्य सभी वैक्टरों की कार्रवाई की एक ही रेखा होती है।.

वैक्टर का उपयोग विभिन्न क्षेत्रों जैसे गणित, भौतिकी, बीजगणित और ज्यामिति में भी प्रतिनिधित्व के रूप में किया जाता है, जहां वैक्टर केवल तभी मिलते हैं जब उनकी दिशा समान होती है, भले ही उनका अर्थ क्या हो.

सुविधाओं

- निर्देशांक के बीच संबंध बराबर होने पर दो या दो से अधिक वैक्टर का मिलान होता है.

उदाहरण 1

हमारे पास वैक्टर m = m_x है; m_y और n = n_x; n_y। ये मिलीभगत हैं अगर:

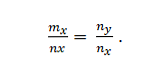
उदाहरण 2

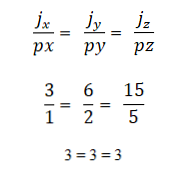
- यदि उत्पाद या वेक्टर गुणन शून्य (0) के बराबर है, तो दो या अधिक वैक्टर टकराने लगते हैं। ऐसा इसलिए है, क्योंकि समन्वय प्रणाली में, प्रत्येक वेक्टर को अपने संबंधित निर्देशांक की विशेषता होती है, और यदि ये एक दूसरे के आनुपातिक होते हैं, तो वैक्टर का संपर्क टूट जाएगा। इसे निम्नानुसार व्यक्त किया जाता है:

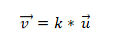
उदाहरण 1

हमारे पास वैक्टर a (10, 5) और b = (6, 3) हैं। यह निर्धारित करने के लिए कि क्या वे समतल हैं, निर्धारक सिद्धांत लागू किया जाता है, जो क्रॉस उत्पादों की समानता स्थापित करता है। इस तरह, आपको निम्न करना होगा:

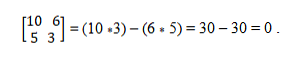
कोलिनियर वेक्टर प्रणाली

कोलिनियर वैक्टर को इन-कॉन्सिडिरिंग की दिशा और अर्थ का उपयोग करते हुए रेखीय रूप से दर्शाया जाता है कि उन्हें आवेदन के बिंदु से गुजरना चाहिए- और मॉड्यूल, जो एक निश्चित पैमाने या लंबाई है.

कोलीनियर वैक्टर की प्रणाली तब बनती है जब दो या दो से अधिक वैक्टर किसी वस्तु या शरीर पर कार्य करते हैं, एक बल का प्रतिनिधित्व करते हैं और उसी दिशा में कार्य करते हैं.

उदाहरण के लिए, यदि एक शरीर पर दो संपीड़ित बल लागू होते हैं, तो इनका परिणाम केवल उस दिशा पर निर्भर करेगा जिसमें वे कार्य करते हैं। तीन मामले हैं, जो हैं:

विपरीत इंद्रियों के साथ कोलिनियर वैक्टर

दो कोलीनियर वैक्टर का परिणाम इनके योग के बराबर होता है:

आर = = एफ = एफ₁ + एफ_2.

उदाहरण

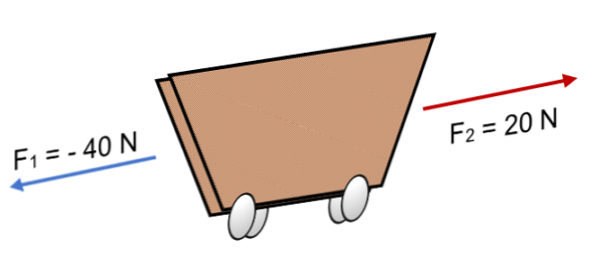
यदि दो बल एक गाड़ी F पर कार्य करते हैं₁ = 40 एन और एफ₂ = 20 एन विपरीत दिशा में (छवि में दिखाया गया है), परिणाम है:

आर = N एफ = (- 40 एन) + 20 एन.

आर = - 20 एन.

कोलिनियर वैक्टर समान भाव से

परिणामी बल का परिमाण कोलिन वैक्टर के योग के बराबर होगा:

आर = = एफ = एफ₁ + एफ_2.

उदाहरण

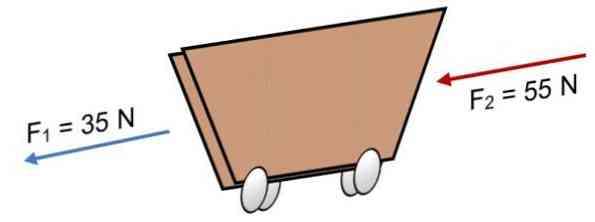
यदि दो बल एक गाड़ी F पर कार्य करते हैं₁ = 35 एन और एफ₂ = 55 एन उसी दिशा में (जैसा कि छवि में दिखाया गया है), परिणाम है:

आर = Σ एफ = 35 एन + 55 एन.

आर = 90 एन.

सकारात्मक परिणाम इंगित करता है कि कोलियर वैक्टर बाईं ओर कार्य करता है.

समान परिमाण और विपरीत इंद्रियों के साथ कोलिनियर वैक्टर

दो कोलीनियर वैक्टर का परिणाम कोलिनियर वैक्टर के योग के बराबर होगा:

आर = = एफ = एफ₁ + एफ_2.

चूंकि बलों में समान परिमाण होता है, लेकिन विपरीत दिशा में होता है, एक सकारात्मक होगा और दूसरा नकारात्मक-, जब दोनों बलों को जोड़ते हैं तो परिणामी शून्य के बराबर होगा.

उदाहरण

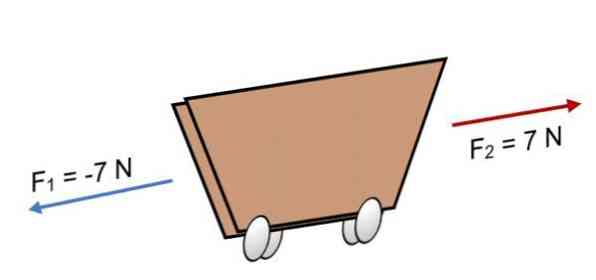
यदि दो बल एक गाड़ी F पर कार्य करते हैं₁ = -7 एन और एफ₂ = 7 एन, जिसमें समान परिमाण है लेकिन विपरीत दिशा में (जैसा कि छवि में दिखाया गया है), परिणाम है:

आर = N एफ = (-7 एन) + 7 एन.

आर = 0.

चूंकि परिणामक 0 के बराबर है, इसका मतलब है कि वैक्टर एक दूसरे के खिलाफ संतुलित हैं और इसलिए, शरीर संतुलन में है या आराम से (यह नहीं चलेगा).

कोलिनियर और समवर्ती वैक्टर के बीच अंतर

कोलिनियर वैक्टर को एक ही रेखा पर एक ही दिशा होने की विशेषता है, या क्योंकि वे एक रेखा के समानांतर हैं; यही है, वे वैक्टर प्रत्यक्ष समानांतर रेखाएं हैं.

दूसरी ओर, समवर्ती वैक्टर को परिभाषित किया जाता है क्योंकि वे कार्रवाई की विभिन्न लाइनों में होते हैं जो एक ही बिंदु में अवरोधन होते हैं.

दूसरे शब्दों में, उनके मूल या आगमन का एक ही बिंदु है - उनके मॉड्यूल, दिशा या दिशा की परवाह किए बिना -, उनके बीच एक कोण का निर्माण.

समवर्ती वैक्टर की प्रणाली गणितीय तरीकों या ग्राफ द्वारा हल की जाती है, जो बलों के समांतर चतुर्भुज की विधि और बलों के बहुभुज की विधि है। इन के माध्यम से एक परिणामी वेक्टर का मान निर्धारित किया जाएगा, जो उस दिशा को इंगित करता है जिसमें एक शरीर हिल जाएगा.

मूल रूप से, कोलिनियर वैक्टर और समवर्ती वैक्टर के बीच मुख्य अंतर कार्रवाई की रेखा है जिसमें वे कार्य करते हैं: कोलिनियर एक ही लाइन में कार्य करते हैं, जबकि समवर्ती भिन्न.

यही है, कोलिनियर वैक्टर एक एकल विमान, "एक्स" या "वाई" में कार्य करते हैं; और एक ही बिंदु से शुरू होने वाले दोनों विमानों में समवर्ती अधिनियम.

कोलिनियर वैक्टर एक बिंदु में नहीं हैं, जैसा कि समवर्ती वाले करते हैं, क्योंकि वे एक दूसरे के समानांतर हैं.

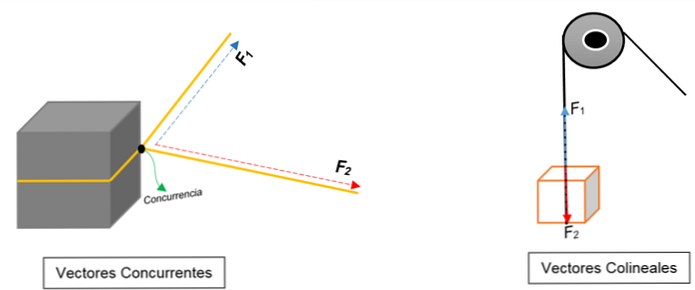
बाईं छवि में आप एक ब्लॉक देख सकते हैं। इसे रस्सी से बांधा जाता है और गाँठ इसे दो भागों में विभाजित करती है; जब विभिन्न झुकावों और विभिन्न बलों के साथ खींचा जा रहा है, तो ब्लॉक एक ही दिशा की ओर बढ़ेगा.

दो वैक्टर का प्रतिनिधित्व किया जाता है कि एक बिंदु (ब्लॉक) में उनके मॉड्यूल, भाव या दिशा की परवाह किए बिना.

इसके बजाय, सही छवि में एक चरखी दिखाई देती है जो एक बॉक्स को उठाती है। रस्सी कार्रवाई की रेखा का प्रतिनिधित्व करती है; जब इसे खींचा जाता है, तो दो बल (वैक्टर) इस पर कार्य करते हैं: तनाव का एक बल (ब्लॉक पर चढ़ते समय) और दूसरा बल, वह जो ब्लॉक के वजन को बढ़ाता है। दोनों की दिशा समान है लेकिन विपरीत दिशाओं में है; एक बिंदु में सहमत नहीं है.

संदर्भ

1. एस्टेला, जे। जे। (1988)। वेक्टर विश्लेषण। खंड 1.
2. गुप्ता, ए। (S.f.)। टाटा मैकग्रा-हिल एजुकेशन.
3. जिन हो क्वाक, एस। एच। (2015)। रेखीय बीजगणित। स्प्रिंगर विज्ञान और व्यापार मीडिया.
4. मोंटिएल, एच। पी। (2000)। टेक्नोलॉजिकल बैकलोरिएट के लिए भौतिकी 1। पटैरिया संपादकीय समूह.
5. सैंटियागो बर्बैनो डी एरसीला, सी। जी। (2003)। सामान्य भौतिकी संपादकीय टेबर.
6. सिन्हा, के। (S.f.)। गणित की बारहवीं कक्षा की एक पाठ्य पुस्तक। 2. रस्तोगी प्रकाशन.