एक सर्कल में समरूपता के कितने अक्ष हैं?

एक वृत्त की सममिति अक्ष वे अनंत हैं। ये अक्ष वे हैं जो किसी भी ज्यामितीय आकृति को दो समान बराबर हिस्सों में विभाजित करते हैं.

और एक वृत्त में वे सभी बिंदु होते हैं जिनकी एक निश्चित बिंदु से दूरी एक निश्चित मान "r" से कम या बराबर होती है.

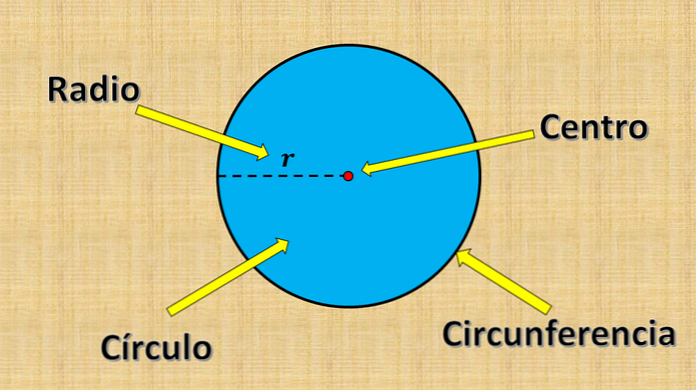
ऊपर वर्णित निश्चित बिंदु को केंद्र कहा जाता है, और "आर" मान को त्रिज्या कहा जाता है। त्रिज्या सबसे बड़ी दूरी है जो सर्कल और केंद्र के एक बिंदु के बीच हो सकती है.

दूसरी ओर, कोई भी रेखा खंड जिसका सिरा वृत्त (परिधि) के किनारे पर होता है और केंद्र से होकर गुजरता है, व्यास कहलाता है। इसकी माप हमेशा दो बार त्रिज्या के बराबर होती है.

घेरा और परिधि

एक सर्कल के साथ एक सर्कल को भ्रमित न करें। परिधि केवल उन बिंदुओं को संदर्भित करती है जो केंद्र से दूरी "आर" पर हैं; वह है, केवल चक्र का किनारा.

हालाँकि, जब आप एक वृत्त के साथ या एक चक्र के साथ काम करते हैं, तो समरूपता के अक्षों की तलाश करना उदासीन है.

समरूपता का एक अक्ष क्या है?

समरूपता का एक अक्ष एक रेखा है जो दो समान भागों में एक निश्चित ज्यामितीय आकृति को विभाजित करता है। दूसरे शब्दों में, समरूपता का एक अक्ष दर्पण की तरह कार्य करता है.

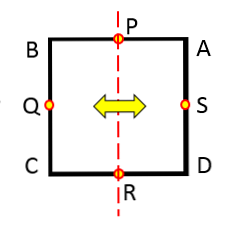
एक वृत्त की समरूपता के शाफ्ट

यदि आप इसकी त्रिज्या की परवाह किए बिना किसी भी वृत्त का निरीक्षण करते हैं, तो आप देख सकते हैं कि यह पार करने वाली प्रत्येक रेखा समरूपता का एक अक्ष नहीं है.

उदाहरण के लिए, निम्न छवि में खींची गई कोई भी रेखा समरूपता की धुरी नहीं है.

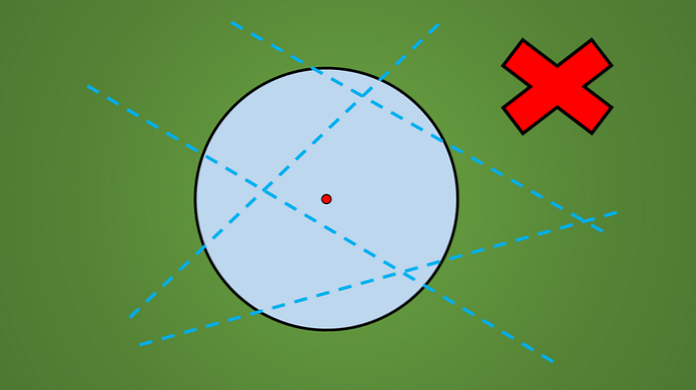
यह जांचने का एक आसान तरीका है कि क्या रेखा सममिति की धुरी है या नहीं, यह लंबवत ज्यामितीय आकृति को रेखा के विपरीत दिशा में परावर्तित करना है।.

यदि प्रतिबिंब मूल आकृति के साथ फिट नहीं होता है, तो वह रेखा समरूपता की धुरी नहीं है। निम्न छवि इस तकनीक को दर्शाती है.

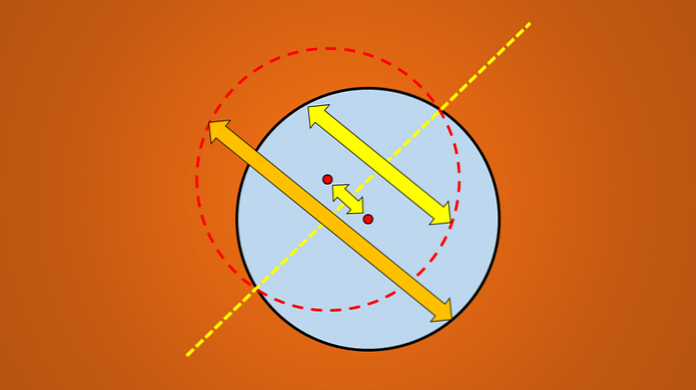
लेकिन यदि निम्न छवि पर विचार किया जाता है, तो यह सर्वविदित है कि खींची गई रेखा वृत्त की समरूपता का एक अक्ष है.

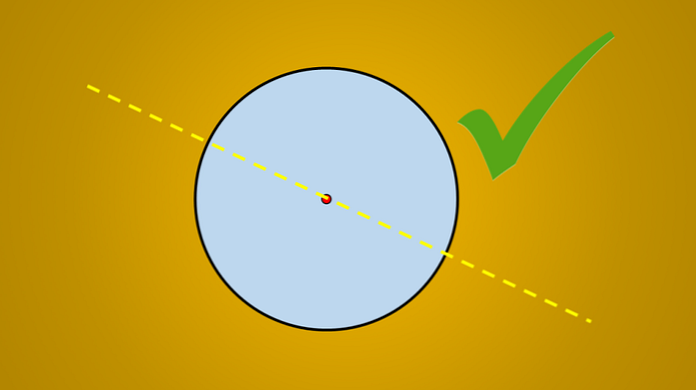
सवाल यह है: क्या समरूपता के अधिक अक्ष हैं? जवाब है हां। यदि आप इस रेखा को 45 ° वामावर्त घुमाते हैं, तो प्राप्त रेखा वृत्त की समरूपता का एक अक्ष भी है.

यदि आप 90 °, 30 °, 8 ° और, सामान्य रूप से, किसी भी संख्या में डिग्री को घुमाते हैं, तो ऐसा ही होता है.

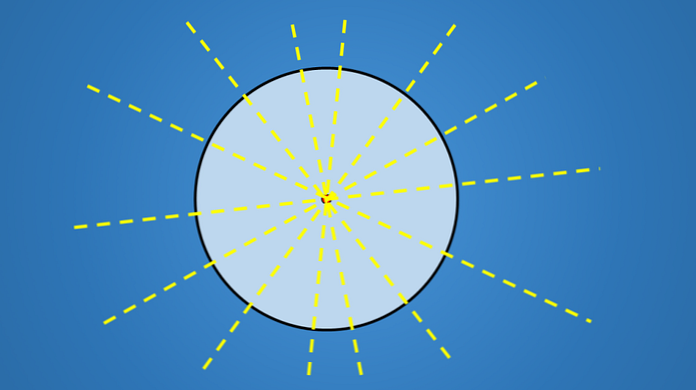
इन पंक्तियों के बारे में महत्वपूर्ण बात यह नहीं है कि उनके पास झुकाव है, लेकिन वे सभी सर्कल के केंद्र से गुजरते हैं। इसलिए, किसी भी रेखा में चक्र का एक व्यास होता है जो समरूपता का एक अक्ष है.

इसलिए, चूंकि एक वृत्त में अनंत संख्या में व्यास होते हैं, तो इसमें सममिति के अक्षों की अनंत संख्या होती है.

अन्य ज्यामितीय आकृतियाँ, जैसे कि एक त्रिभुज, एक चतुर्भुज, एक पंचभुज, एक षट्भुज या कोई अन्य बहुभुज, सममिति के अक्षों की परिमित संख्या होती है.

एक सर्कल में सममिति के अक्षों की अनंत संख्या होने का कारण यह है कि इसका कोई पक्ष नहीं है.

संदर्भ

1. बास्तो, जे। आर। (2014). गणित 3: बुनियादी विश्लेषणात्मक ज्यामिति. पटैरिया संपादकीय समूह.
2. बिलस्टीन, आर।, लिब्सेकिंड, एस।, और लोट, जे। डब्ल्यू। (2013). गणित: बेसिक शिक्षा शिक्षकों के लिए एक समस्या को हल करने का तरीका. लोपेज़ मेटोस एडिटर्स.
3. बॉल्ट, बी। और हॉब्स, डी। (2001). मैथ लेक्सिकॉन (सचित्र संस्करण।) (एफ। पी। कैडेना, ट्रेड।) संस्करण एकेएल.
4. कैलेज़ो, आई।, एगुइलेरा, एम।, मार्टिनेज, एल।, और एल्डिया, सी। (1986). गणित। ज्यामिति। E.G.B के ऊपरी चक्र का सुधार. शिक्षा मंत्रालय.
5. श्नाइडर, डब्ल्यू।, और सपर्ट, डी। (1990). व्यावहारिक तकनीकी ड्राइंग मैनुअल: औद्योगिक तकनीकी ड्राइंग की मूल बातें परिचय. Reverte.
6. थॉमस, जी। बी। और वीर, एम। डी। (2006). गणना: कई चर. पियर्सन शिक्षा.